LabSim

A expressão , é a forma geral implícita de uma equação diferencial ordinária de ordem n, na variável dependente , tendo como variável independente x. Se esta equação for resolvida em ordem à derivada de  de ordem mais elevada origina a seguinte equação

(55)

que em conjunto com as suas n condições iniciais , definem um problema com condições iniciais, que tem solução única no intervalo [a, b].
Para se poder resolver um problema com condições iniciais como aquele definido na expressão (40), é necessário transformar a equação diferencial de ordem n em um sistema de n equações diferenciais de primeira ordem. Para se conseguir efectuar esta transformação é necessário definir n-1 novas variáveis dependentes. Assim designando  por ,

, (56)

E fazendo agora o mesmo para as outras variáveis dependentes, estas ficam definidas da seguinte maneira:

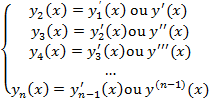(57)

As condições iniciais passam então a ser
Assim o sistema de n equações diferenciais de primeira ordem resultante da definição das novas variáveis, e que é equivalente à equação diferencial de ordem n definida anteriormente, tem a seguinte forma

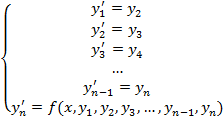  (58)

Onde a função  é a função que define a equação diferencial de ordem superior.
Agora para resolver este sistema, apenas é necessário aplicar o algoritmo para resolução de equações diferenciais (já referido em outra secção), como se faria para outro sistema de equações diferenciais ordinárias de primeira ordem.