LabSim

Equações de Runge-Kutta e esquemas preditores-correctore

 

Qualquer dos métodos referidos anteriormente para resolução de uma equação diferencial de primeira ordem com condições iniciais, pode ser usado para a resolução de um sistema de n equações diferenciais de primeira ordem com condições iniciais.
Para se usar os métodos já falados em sistemas de equações diferenciais com condições iniciais deve-se seguir a seguinte estratégia:

• Implementar a equação diferença do método a cada uma das equações do sistema, com atenção a equação 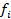 que define a equação i do sistema. Definindo-se assim uma solução constituída por uma família de valores, 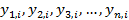, gerada passo a passo,  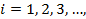das mesma maneira como se fazia para uma só equação.

Embora a implementação das fórmulas numéricas não tenha grandes dificuldades, no método de Runge-Kutta e nos métodos preditores-correctores, é necessário ter em atenção a ordem com que os cálculos são efectuados. Por exemplo:

• Para implementar o método de Runge-Kutta de segunda ordem, as equações a serem usadas para a resolução de um sistema de n equações diferencias, para o passo i (i=0,1, …) são

 ,   (40)
,    (41)
…, e
  (42)
em que
,   (43)
, (44)
,  (45)
,  (46)
  (47)
e
.   (48)

Os cálculos devem começar pelos valores de , visto estes serem necessários para o calculo dos valores de , que são calculados a seguir, e por ultimo devem ser calculados os valores dos  de cada equação, referentes ao passo i.

• Para a implementação do método preditor-corrector de Adams de segunda ordem, são necessárias duas fórmulas para cada equação do sistema.

,    (49)
,  (50)
      (51)
,  (52)
…
e
,   (53)
.   (54)

Cada valor corrigido tem de ser calculado em função dos valores previstos de todas as n variáveis dependentes, logo, os cálculos devem ser começados pelos valores previstos , calculando-se a seguir os valores corrigidos .