LabSim

Se for possível obter o modelo matemático que descreve o sistema em estudo, então é possível obter o valor dos parâmetros do controlador, que satisfaçam as especificações desejadas para a resposta transitória em regime permanente do sistema em malha fechada. Mas se não for possível obter o modelo matemático do sistema, então é necessário utilizar métodos experimentais par obter os parâmetros do controlador.
Ao processo de seleccionar os parâmetros adequados para responder aos requisitos pretendidos chama-se sintonização [30].

Métodos de Ziegler-Nichols

Ziegler e Nichols criaram um conjunto de regras para sintonizar controladores PID, baseando-se em resultados experimentais. Estas regras, para determinar os valores de ,  e , baseiam-se na resposta transitória do sistema a estudar.

• Ziegler-Nichols em malha aberta

Este método de sintonização, para ser aplicado, necessita que o sistema em malha aberta tenha como resposta a um degrau de amplitude A uma curva do tipo S (curva de reacção do processo). Esta curva pode ser obtida experimentalmente ou por simulação.
Neste método o sistema pode ser aproximado por um sistema de primeira ordem com atraso.

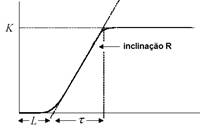
Curva em s

 

A curva pode ser caracterizada pelos parâmetros L (atraso) e τ (constante de tempo). Estes parâmetros são obtidos traçando uma tangente ao ponto de inflexão da curva, e determinando o ponto de intersecção da tangente com o eixo do tempo.
Obtendo os valores de R e L, pode-se calcular os valores ,  e  através da tabela 2.

 

Tabela 2 - Tabela para cálculo dos parâmetros do controlador PID pelo método de Ziegler-Nichols em malha aberta

• Ziegler-Nichols em malha fechada

 

Neste método de sintonização deve-se colocar o sistema em malha fechada e usar apenas o controlador proporcional. Em seguida aplica-se variação em degrau na referência e vai-se aumentando o ganho do controlador até se obter na saída uma resposta oscilatória, figura 18. A frequência de oscilação é a frequência crítica, Wco.
Pode-se calcular então os valores do ganho último e do período último.

Ganho último:    (74) 

Período último:   (75)

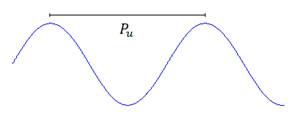
Oscilação constante com período Pu

 

Com os valores de  e , já se pode obter os valores de ,  e , através da tabela 3.

Tabela 3 - Tabela para cálculo dos parâmetros do controlador PID pelo método de Ziegler-Nichols em malha fechada