LabSim

Neste sistema, existem duas molas, mas apenas uma delas está ligada ao corpo de massa m. Então é necessário designar dois pontos, M e A, onde as forças vão ser aplicadas. 

Força elástica duas molas

Pela lei de Newton sabe-se que 

    (1)

A força de atrito e força elástica são iguais a

   (2)
   (3)
     (4)

onde n=1,2…

No ponto M estão aplicadas a força F, a força de atrito FB1 e a força elástica Fk1. Logo a equação para o ponto M é

    (5)

Substituindo FB1 e Fk1 na equação (5), pelas suas expressões, obtém-se

   (6)

Colocando a derivada de maior ordem em evidência,

   (7)

No ponto A são aplicadas a força elástica Fk1, a força elástica Fk2 e a força de atrito FB2. Logo para o ponto A tem-se a equação

   (8)

Substituindo Fk1, Fk2 e FB2, pelas suas expressões na equação (8), obtém-se

     (9)

Resolvendo em ordem à derivada de maior grau

     (10)

Para converter as equações diferenciais (7) e (10), em um sistema de equações de primeira ordem é necessário efectuar as seguintes mudanças de variável.

Assim, obtém-se o seguinte sistema de equações diferenciais.

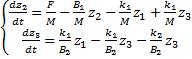      (11)

Colocando em notação espaço de estados.

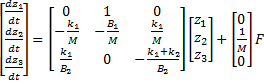      (12)

Escolhendo como variáveis de saída o deslocamento  e o deslocamento .

Logo

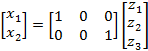       (13)