Plano inclinado
Neste caso, existe um corpo de massa M a subir um plano inclinado com um determinado ângulo θ. Este corpo está sujeito à força F, à força gravítica P, à força de atrito Fa e a força de reacção R.
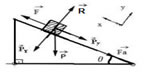
Plano inclinado
Pela lei de Newton sabe-se que
(1)
Para este sistema consideram-se a projecção das forças aplicadas segundo o eixo dos x e segundo o eixo dos y.
Segundo o eixo dos x estão aplicadas ao corpo a força F a força de atrito Fa e a força gravítica segundo x Px.
Pela lei de Newton.
(2)
Onde
(3)
(4)
e
(5)
Substituindo as equações (3), (4) e (5) em (6) tem-se
(6)
Colocando a equação (6) em ordem à sua derivada de maior grau, obtém-se a equação diferencial que descreve o sistema segundo o eixo dos x
(7)
Segundo o eixo dos y são aplicadas ao corpo a força gravítica segundo y Py e a força de reacção normal R.
Normalmente, nestes sistemas a força R e a força Py, têm valores simétricos, logo anulam-se.
(8)
(9)
(10)
Utilizando as seguintes mudanças de variável para as equação segundo x
Obtém-se o sistema de equações diferenciais de primeira ordem que descreve o comportamento do sistema.
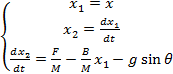(11)
Colocando em notação espaço de estados.
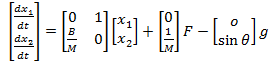(12)
Escolhendo como variável de saída a velocidade (
)
Logo
(13)