Pêndulo invertido
Neste sistema, existe um corpo de massa M que se desloca segundo o eixo dos x, e um pêndulo invertido, de comprimento l e massa m, ligado a parte superior do corpo de massa M e que se pode movimentar segundo o eixo dos x e do eixo dos y.
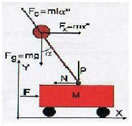
Pêndulo invertido
O pêndulo deve ficar equilibrado, variando a força F aplicada ao corpo de massa M, de maneira a que α tenda para 0.
Para este sistema consideram-se apenas as forças aplicadas segundo o eixo do x.
As forças aplicadas ao corpo M são a força F e a força N.
Logo pela lei de Newton
(1)
(2)
Sabe-se que ,
(3)
Substituindo na equação (2), obtém-se
(4)
Aplicadas ao pêndulo existem a força centrífuga Fc a força F segundo x, Fx, e a Força gravítica segundo x, Fgx.
(5)
(6)
(7)
Pela lei de Newton
(8)
Então substituindo as expressões de Fc, Fx e Fgx na lei de Newton chega-se a
(9)
Observando as equações (6) e (7), vê-se que estas equações não são lineares.
Para tornar o sistema linear, é necessário efectuar algumas aproximações.
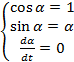(10)
Assim as equações ficam
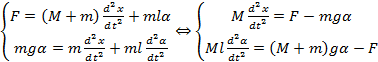(11)
Colocando as equações em ordem à derivada de maior grau obtém-se o seguinte sistema de equações de primeira ordem
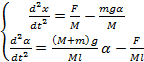(12)
Efectuando as seguintes mudanças de variável
Obtém-se o seguinte sistema de equações
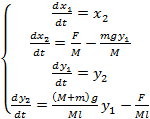(13)
Colocando em notação espaço de estados.
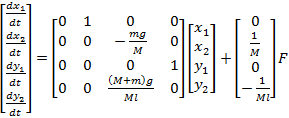(14)
Escolhendo como variáveis de saída o deslocamento x (
) e o ângulo α (
)
Logo
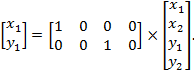(15)