Suspensão Automóvel
O modelo que representa a suspensão de um automóvel é o apresentado na figura.
Ao corpo M1 são aplicadas a força elástica Fe1, a força de atrito FB e a força gravítica Fg1.
Ao corpo M2 estão aplicadas a força elástica Fe2, a força gravítica Fg2, e as forças Fe1 e FB
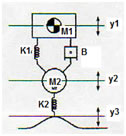
Suspensão automóvel
O sistema de equações diferenciais que descreve o comportamento deste sistema é o sistema de equações (1). Onde M1 e M2 são a massas dos dois corpos presentes, K1 e K2 são as constantes de elasticidade das duas molas e B é o coeficiente de amortecimento.
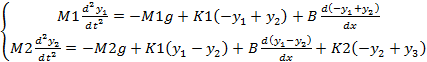(1)
Resolvendo em ordem à derivada de maior grau de cada equação
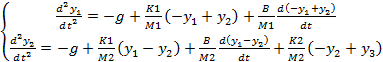(2)
Efectuando as seguintes mudanças de variável
Obtém-se o seguinte sistema de equações diferenciais de primeira ordem.
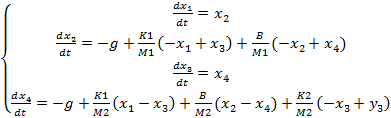(3)
Colocando em notação espaço de estados.
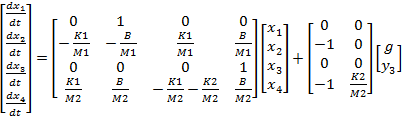(4)
Escolhendo como variáveis de saída o deslocamento 
(
) e o deslocamento 
(
)
Logo
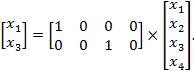(5)